情報系専門学校生がつまづく計算問題 | 指数と補数の勘違い

国家試験「基本情報技術者試験」の科目A（昔の午前問題）を通過するか/否かは、計算問題に立ち向かうか/捨てるかは大きな一因です。

例えば午前問題時代、問題は80問。合格点は60%、計算問題を10問とすると。

• 計算問題に立ち向かえば…60/80問=60%正解すれば通過
• 計算問題を捨て問にすれば…60/70問=86%正解すれば通過

「計算問題だ。解かないぞ。」と、最初から切ってるとハードルが高くなっていくだけです。

専門学校には、割り算できない学生はいます、3桁の掛け算ができない学生もいます。

そのことは構わないのですが、しっかり向き合うよう指導はします。

得点できなくても立ち向かえば良いと思っています。

「計算が苦手でー」「英語が苦手でー」と避け続けて諦めて、「捨て問」にして考えをやめてしまいます。

• 立式ができなければ、現実問題のプログラム化ができません
• 英語が単語レベルでできなければ、プログラムが組めません

計算問題の中でも、「指数」「補数」が最初で最後の難関です。

今回は、情報系1年生に授業をして、学生さんの勘違いから思ったことを書いてみます。

学習者の方は勘違いをしていないかの理解を、教育者の方は教え方の参考になれば嬉しいです。

累乗問題では「2の2乗」で混乱しちゃう

指数計算は、資格でも実務でも使います。

• 進数変換…「10進数を2進数になおしなさい」問題
• IPアドレスの計算…サブネットマスク、IPアドレスの数の問題

指数計算が一番多い間違いが、「2の0乗が0」です。正解は「2の0乗は1」です。

指数計算はできますか？

問題が悪かったなぁと思うとこです。

学生に下記を計算させてみましょう。

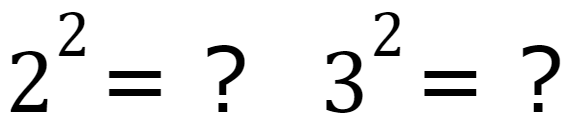
こんな計算をする学生はいませんか？

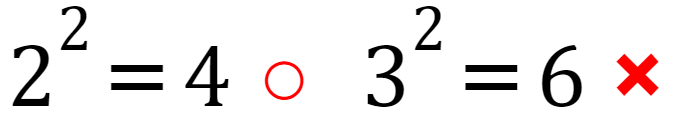
正しい答えは、「3を2回かけるので・・・」ってことで、

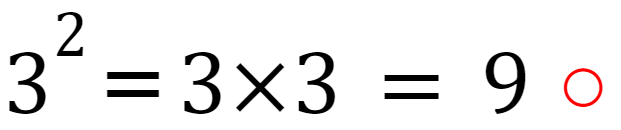
ということで、

「掛け算で考えても、累乗で考えても成立してしまう数はダメ」ですねｗ

さて、プログラムで確認してみましょう。pythonです。

1から29の数字2つを、掛け算した値と累乗した値を比べて、両方が一致した時にその数を表示します。

google colaboratoryなどで試してみてください。

for a in range(1,30):
  for b in range(1,30):
    if a*b==a**b:
      print(f"{a} {b}")

計算結果で、2×1=2の1乗、29×1=29の1乗というのはいっぱいでますが、それは無視するとして。

2×2=2の2乗ってのも出ますね。なので計算法の勘違いでも正解しちゃう唯一の例です。

1 1
2 1
2 2
3 1
4 1
5 1
6 1
7 1
8 1
9 1
10 1
11 1
12 1
13 1
14 1
15 1
16 1
17 1
18 1
19 1
20 1
21 1
22 1
23 1
24 1
25 1
26 1
27 1
28 1
29 1

ということで、2の2乗だけを避ければ良さそうです。

累乗では下記もおさえてほしいですね。

まず下記は不思議な式かもしれませんが、進数変換でばっちり使います。

広がる累乗の世界　～マイナスの指数、小数の指数～

「2の0乗=1」の理由は最初は教えていたんですが、もう授業中には説明はしないようになりました。

学生さんは「結局覚えればいいじゃん」「（今はとりあえず）解けれるようになればいいじゃん」と思うようです。その気持ちもわかりますから。

授業時間も圧迫されるし、純粋数学の授業ではなく、情報系の計算の授業ですからね。

無念なとこはありますが、そう言い聞かせます。

さらにせっかくだから、下記も理解してほしいなぁ。

• 2の-1乗=1/2=0.5
• 2の0.5乗=√2=1.4.1421356・・・
• 27の1/3乗=三乗根の27=3

これらは、指数計算が「指数の四則演算」でできることを理解してもらえば良いのですが・・・

なかなか難しいようですｗ

モノを数えることで生まれた「数」は、数学という「ルール」になった

数って「りんごが何個」とか現実の物体と紐づいていると思うので、累乗や-1乗とかの想像がつかないのかもしれません。

「リンゴが2の-1乗個」なんて言いませんもんね。

数は物を数えることから始まったと思います。

その考えを小数点や負数に広げて「数として成り立つルール」が数学だと思っています。

虚数についても実体験につながらないのでしょう。

でも、そのおかげで、電子回路とか正弦波とかが表現できるということは知ってもらいたい。

ただ、一概に「ダメだなぁ」とは言えません。つい、言いたくなるし、言ってしまうことはあります。

でも、一般相対論でテンソルで頭おかしくなるのと同じですよきっと。

共変テンソル、反変テンソル・・・うっ頭が。

「２の補数」でのビット反転の「反転」で勘違いしちゃう

進数変換を何とか乗り越えても、「補数」は超難関です。

まぁ。資格でも1問でるかでないかなので、学習効果は薄いんですが。今では必要になるのは、マイコンを使う時ぐらいですかね。

正直みんな間違うので期末テストでも配点を低くしてます。

「2の補数」を教えた時の勘違い

教え方が悪かったなぁと思うとこです。

「2の補数」を計算するには、「反転して+1する」と教えるんですが勘違いが発生。

私達がやってほしいのは「ビット反転」なんですが、

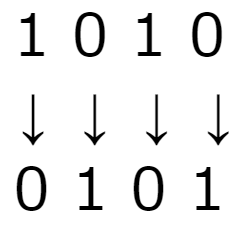
「左右反転」と解釈されたことがあります。

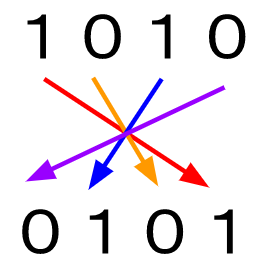
たしかにその通りです。

ビット反転でも左右反転でも同じ解になるは避けないとですね。

「各桁の、0を1に、1を0に、変える」と言わないといかんのでしょうね。

「0と1を反転」とすると、ある桁の0と別の桁の1を入れ替えるとかしそうｗ

教えるって難しいですね。

教えるのは難しい、教え続けて成長してもらおう

とはいえ、あれやこれやとデラックスに教えても、頭パンクしちゃうでしょうし、端折りすぎても伝わらないし、本質的な理解につながりません。

累乗でも触れたように、本質的な理解の学習コスト、学生が感じる興味や必要性もあります。

板書で色を変えたりして伝えても、「計算だー」と思考停止していたら伝わりません。

そしてすぐ忘れます。残念ながらすぐ忘れます。

それも責められないです。もちろん「キー」ってなりますが。

でも、私も「相対性理論」を分かったつもりになって、何度振り出しに戻ったことかと思います。

授業中に「分かった」「解けた」と思わせるってのは学生の満足度になるわけです。

ちょっとずつ成長してもらいましょ。

もちろん数学的にもコンピュータのしくみとしても面白いと思っています。

最後に | 計算問題に立ち向かう学生になってね！

ここまで読んで頂きありがとうございます！

できなくても良いので捨てさせないように、立ち向かうように指導したいですね。

できるようになる学生もときたーまいますし、できないままが大半かもしれません。

それでも、勘違いでもなんでもいいから「立ち向かうことができる人間」になってほしいです。

もちろんパソコンでは、進数変換も補数計算もやってくれます。

それでも机上で設計したり、その場で計算しないといけない場面が職場であると思います。

学生さんに問います。

「２進数への変換やIPアドレスの計算ができない技術者が作ったプログラムやシステムを、使いたいかい？信用できるかい？」

こんな数学や英語によって、便利な機械を人間が作ったのに。使う人間は「数学は電卓、英語は翻訳AI、プログラムはChatGPTでOK。学習する必要なし！」なんて言ってるのは、とても滑稽だなと思っています。

確かに昔の色んな天才さんたちが作り上げた数学なので難しいです。とはいえ、私たちは彼らを超えた知識と機械を使える立場にあるんです。

コンピュータもない頃の人たちを考えると、「彼らにこそコンピュータを届けてあげたい。ぼくなんかより有効に使ってくれるだろう」と申し訳ない気持ちになります。

※差別や侮蔑だと感じられたらごめんなさい。