今回は、プログラムの関数化・統計・グラフ描画などを組み合わせた実習をします。
▼事前に読んで欲しい記事▼
問題
1年は365日または366日ありますが、何人集まれば誕生日が同じ人が出るかな、という問題。
なんと23名いれば50%の確率で誕生日が同じペアが現れるとのことです。
200人ぐらい必要かなと思うところですが、すごく少なくてびっくりしますね。
ってことで、今回は確率と統計にチャレンジしてみましょう(参考サイト)。
課題1~5で、23名いれば確率50%で同じ誕生日の人がいそうってことを計算します。
課題6~7で、下記のグラフを描いてみます。
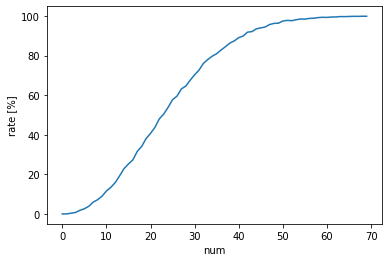
横軸23ぐらいのところが、縦軸50ぐらいになっていることがわかりますかね。。。w
課題1:誕生日を発生させる
乱数を使って誕生日を発生させます。
誕生日は「何月何日」ですが、お正月から何日目ということにしましょう。
1月1日を1日目、12月31日を365日目という感じです。
乱数を使ってみよう
課題は下記です。
- 1~365からランダムで1つ数字を表示する
- 上の処理を10人分だけ繰り返す。
- 乱数はrandint()を使ってください。
答えは下記な感じです。
import random
arr=[]
for i in range(0,10):
days=random.randint(1,365)
print(days)118
247
82
156
146
12
264
80
218
138関数化する
使いやすくするために関数にしてみましょう。
課題は下記です。
- create_birthdayという関数にしなさい
- 引数は、計算する人数で、変数はnumとします。
- 返値は、生成された誕生日が格納された、一次元リストとします。
作った関数を呼び出してみましょう。
- create_birthdayを呼び出して、10人の誕生日を生成して表示させなさい。
import random
def create_birthday(num):
arr=[]
for i in range(0,num):
days=random.randint(1,365)
arr.append(days)
return arr
ans=create_birthday(10)
print(ans)[341, 278, 242, 185, 206, 303, 71, 198, 58, 99]課題2:同じ誕生日があるか調べる
リストの中のデータで同じ数値があるかを判別するプログラムを作ります。
同じ誕生日があったら表示する
課題文は下記です。
- arr = [30, 12, 3, 12, 234] を読み込んだら、以下が表示される。
- same birth-day 12 : 1 & 3
- same birth-day 12 : 3 & 1
arr = [30, 12, 3, 12, 234]
for i in range(0,len(arr)):
for j in range(0,len(arr)):
if i != j:
if arr[i] == arr[j]:
print(f"same birth-day {arr[i]} : {i} & {j}")same birth-day 12 : 1 & 3
same birth-day 12 : 3 & 1二重にでているのは、次で改良しましょう。
同じ誕生日があったら表示する改
課題文です。
- 二重に表示されているのを1つにしてください。
same birth-day 12 : 1 & 3答えは下記です。
arr = [30, 12, 3, 12, 234]
for i in range(0,len(arr)):
for j in range(i,len(arr)): ### 改善する箇所
if i != j:
if arr[i] == arr[j]:
print(f"same birth-day {arr[i]} : {i} & {j}")
jをiにしても、j=iって自分自身の比較はif文でしないようになっているので、
jをi+1にすれば良いです。
arr = [30, 12, 3, 12, 234]
for i in range(0,len(arr)):
for j in range(i+1,len(arr)): ### こっちでもOK。
if i != j:
if arr[i] == arr[j]:
print(f"same birth-day {arr[i]} : {i} & {j}")関数にする
使いやすくするために関数にしてみましょう。
課題文は下記です。
- 関数名は judge_sameday() とする。
- 引数はリスト arr とする。
- 返値は
- 同じ日がなければ、0とする。
- 同じ日があれば、1とする。
作った関数を呼び出してみましょう。
- arr = [30, 12, 3, 12, 234]とする。
- judge_sameday(arr)を呼び出す。
- 返値を受けて、表示する。1が表示されるはずです。
def judge_sameday(arr):
flag=0 ###########################
for i in range(0,len(arr)):
for j in range(i+1,len(arr)):
if i != j:
if arr[i] == arr[j]:
flag=1 ##################
return flag #####################
arr = [30, 12, 3, 12, 234]
ans = judge_sameday(arr)
print(ans)1課題3:2つの関数を使ってみる
課題1と2で完成した関数を組み合わせて使ってみましょう。
課題文は下記です。
- create_birthday() と judge_sameday()を使ってください。
- 23人の時に、同じ誕生日の人がいれば1を表示、いなければ0を表示してください。
- 3行以内でできるはずです。
課題1と2で完成した関数を一応載せておきます。
import random
def create_birthday(num):
arr=[]
for i in range(0,num):
days=random.randint(1,365)
arr.append(days)
return arr
def judge_sameday(arr):
flag=0
for i in range(0,len(arr)):
for j in range(i+1,len(arr)):
if i != j:
if arr[i] == arr[j]:
flag=1
return flag
課題3の答えです。
実行を繰り返して、1が表示されたり、0が表示されたりする確認をしてください。
1と0が大体半分ぐらいの頻度で表示されます。
arr = create_birthday(23)
ans = judge_sameday(arr)
print(ans)課題4:同じ誕生日の人がいる確率を求める
課題3で、出力が1(同じ誕生日がいる)だったり、出力が0(同じ誕生日がいない)だったりしたので、確率を求めることができます。
課題3の計算を100回実行して確率を計算する。
課題文は下記です。
- 課題3のプログラムを100回実行しなさい。
- 同じ誕生日がいる確率を計算しなさい。
- 人数は23人のままでOKです。
cnt = 0
for i in range(0,100):
arr = create_birthday(23)
ans = judge_sameday(arr)
if ans == 1:
cnt += 1
print(f"{cnt/100*100}")
表示は、50周辺になるはずです。
47.0関数化する
使いやすくするために関数にしましょう。
課題文は下記です。
- 関数名は ave_sameday_rate()とします。
- 引数はnum。考える人数です。
- 返値は同じ誕生日の人がいる確率です。
関数を呼び出してみましょう。
- 考える人数は23人でOKです。
def ave_sameday_rate(num):
cnt = 0
for i in range(0,100):
arr = create_birthday(num)
ans = judge_sameday(arr)
if ans == 1:
cnt += 1
return cnt/100*100
print(ave_sameday_rate(23))52.0課題5:課題4の計算を繰り返し平均を算出する。
課題4によって、ある人数において誕生日が同じ人が現れる確率が計算できるようになりました。
50%周辺の値がでていますが、揺れが大きいですね。
なので、確率計算をたくさんして、平均をとってみましょう。
確率の平均を計算する
課題文は下記です。
- 課題4のave_sameday_rate()を100回して、確率の平均値を計算しなさい。
sum = 0
for i in range(0,100):
ans = ave_sameday_rate(23)
sum += ans
print(sum/100)
課題4では、確率が50%から5%以上揺れていましたが、
今回平均をとることで、50%から1%程度の揺れに改善されましたね。
なんども実行して確認してみてください。
51.08関数化する
使いやすいように関数にしましょう。
課題文は下記です。
- 関数名は statics_ave_sameday_rate()です。
- 引数はnum。考える人数です。
- 返値は確率の平均値です。
関数の呼び出しもしてください。
- statics_ave_sameday_rate()を呼び出してください。
- 考える人数は23名でOKです。
def statics_ave_sameday_rate(num):
sum = 0
for i in range(0,100):
ans = ave_sameday_rate(num)
sum += ans
return sum/100
ans=statics_ave_sameday_rate(23)
print(ans)課題6:各人数について計算してみる
課題5で、ある人数で同じ誕生日の人が現れる確率の平均値が計算できました。
ここでは、考える人数を変えていくようにしましょう。
1~23人までの確率をそれぞれ計算する。
課題文は下記です。
- statics_ave_sameday_rate()を用いてください。
- 0~23人の時の、同じ誕生日の人がいる確率の平均値をそれぞれ計算してください。
- 出力結果は下記とします。
0 0.00
1 0.00
2 0.24
3 0.67
4 1.67
5 2.53
6 3.91
7 5.49
8 7.52
9 9.06
10 11.96
11 14.16
12 16.46
13 19.53
14 22.08
15 25.25
16 29.08
17 32.20
18 34.79
19 38.72
20 40.45
21 44.24
22 46.78
23 50.21答えのpythonコードです。
ついでなので、桁表示も合わせてみました。
for i in range(0,24):
ans=statics_ave_sameday_rate(i)
print(f"{i:2d} {ans:6.2f}")課題7:グラフにしてみよう
課題6によって、各人数での確率(の平均値)が計算できたので、グラフにしてみましょう。
計算結果をリストに格納する。
下記を写してもらってOKです。
arr_x=[]
arr_y=[]
for i in range(0,24):
ans=statics_ave_sameday_rate(i)
arr_x.append(i)
arr_y.append(ans)
print(arr_x)
print(arr_y)[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]
[0.0, 0.0, 0.27, 0.81, 1.57, 2.84, 3.78, 5.3, 7.67, 8.9, 11.73, 14.15, 15.9, 19.76, 22.14, 25.45, 27.86, 32.07, 34.72, 37.28, 41.44, 44.87, 47.99, 49.46]
グラフを描いてみましょう
下記を写してもらってOKです。
arr_x=[]
arr_y=[]
for i in range(0,24):
ans=statics_ave_sameday_rate(i)
arr_x.append(i)
arr_y.append(ans)
import matplotlib.pyplot as plt
plt.plot(arr_x, arr_y)
plt.xlabel("num")
plt.ylabel("rate [%]")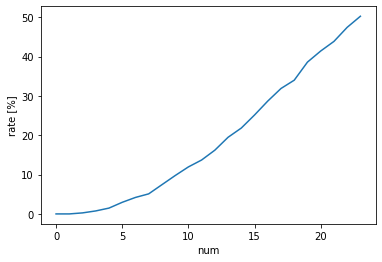
0~70名の計算をして、グラフを描いてみよう
下記を写してOKです。
70名は時間がかかるので、プログレスバーをつけてみました。
from tqdm import tqdm
arr_x=[]
arr_y=[]
for i in tqdm(range(0,70)):
ans=statics_ave_sameday_rate(i)
arr_x.append(i)
arr_y.append(ans)
import matplotlib.pyplot as plt
plt.plot(arr_x, arr_y)
plt.xlabel("num")
plt.ylabel("rate [%]")100%|██████████| 70/70 [01:49<00:00, 1.57s/it]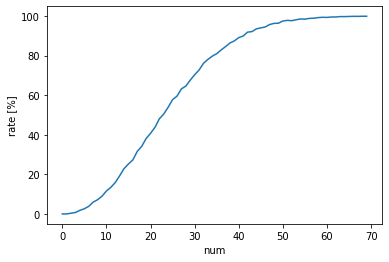
ということで、
23名で50%。40名ぐらいで90%。60名もいれば100%に近い感じですかね。
まとめ
改良について
計算精度を上げるには、とりあえずは、確率計算の100回を増やしたり、確率の平均計算の100回を増やしたりしても良いです。
また、人数が多くなると計算時間が長くなっていることに気づいたと思います。
今回は、全員分の誕生日を生成して、全部のペアを比較しています。
1人生成しては比較、1ペアだけでも同じ誕生日が発見されれば計算を終了、とすると計算時間は短くなると思います。
このあたりも機会があればまた今度!
確率と統計について
確率は、事象を繰り返し計算してカウントして算出します。
一度の計算では値が揺れてしまうので、計算を繰り返して平均値を算出して、揺れ幅を小さくできます。
揺れ幅は標準偏差、平均値の誤差推定値は標準誤差によって算出されますが、今回は割愛しています。
そのあたりは、機会があればまた今度!
まとめ
今回は、誕生日かぶりの不思議な確率をテーマに
Pythonプログラムの基本としては
- 乱数を使う。
- 関数にしてみる。
プログラミングの手順としては、
- プログラムを作っては関数化して使いやすくする。
- グラフの描画をしてみる。
あと、あんまり説明してませんが、
- 統計をやってみる。
って感じでした。


