円周率は、コンピュータでないと計算できないです。
だから、プログラマーとして一度は円周率に挑戦しましょう。
- ライプニッツの公式…無限級数を使った計算
- モンテカルロシミュレーション…乱数を使ったシミュレーション

よろしくー
▼事前に読んで欲しい記事▼
ライプニッツの公式
江戸時代の数学者が導いた数式だゾ!
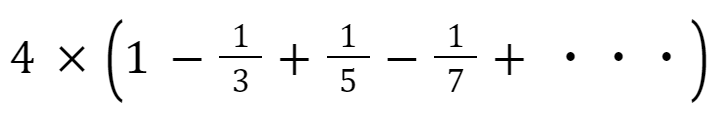
「この式をプログラムで計算してください。絶対知ってる値が出るよ!」
これだけで、プログラムを書いてもらってください。
発見の喜びを体験してもらいましょ。
なんなら、どっかのタイミングで下記を伝えてもOKです。
「1600年代、つまり江戸時代。ドイツの数学者が見つけた公式だよ!」

発見の喜びって大事ー
pythonで作ってみましょう
一応、答えのソース書いておきますが、プログラムの組み方(アルゴリズム)は色々あるし、そこが面白いところです。
学生の「円周率じゃん」という「発見」と「(最適解かはともかく)自分なりにプログラム組めた!」という「体験」や「達成感」みたいなものを感じる機会を奪わないであげましょう。
もちろん最終的には答えを見せて、「写しただけだけど、なんかできた」って体験にしてあげてください。

初めてできたって大事ー
for文とif文を組み合わせた課題として、「奇数だけを足し合わせろ」みたいなのがあると思います。
同じように、奇数だけを取り出すということを考えてもらっても良いですね。
符号をループ毎に正負反転させるところだけ考えればOKです。
sign = 1
sum = 0
for i in range(1,1000000,1):
if i%2 == 1:
sum = sum + sign*1/i
if sign == 1:
sign = -1
else:
sign = 1
sum = sum*4
print(sum)range()の使い方を調べて、1,3,5,7,・・・と2ずつ増やすやり方でもOKですね。
sign = 1
sum = 0
for i in range(1,1000000,2):
sum = sum + sign*1/i
if sign == 1:
sign = -1
else:
sign = 1
sum = sum*4
print(sum)
知ってることを
ちょっとずつ増やそー
残念なpython
正負符号について、負は偶数番目の項なので、別途カウンタ変数cntを設けて数を数えるのもアリです。
sum = 0
cnt = 0
for i in range(1,1000000,2):
cnt=cnt+1
if cnt%2 == 1:
sign = 1
else:
sign = -1
sum = sum + sign*1/i
sum = sum*4
print(sum)
最初はいいんだよー
ただ、pythonでは、enumerate()を使うとカウンタも返してくれます。
ただし、0から数えています。
sum = 0
for cnt,i in enumerate(range(1,1000000,2)):
cnt = cnt+1 # カウンタが1から始まるように細工
if cnt%2 == 1:
sign = 1
else:
sign = -1
sum = sum + sign*1/i
sum = sum*4
print(sum)cntが0から始まることを考慮して、if文の条件を変えてもOKですね。
sum = 0
for cnt,i in enumerate(range(1,1000000,2)):
if cnt%2 == 0: # cntが0から始まるため。
sign = 1
else:
sign = -1
sum = sum + sign*1/i
sum = sum*4
print(sum)下記の動画が参考になります。03:13ぐらいからです。
私はシステムエンジニア出身ではないので、技術者の方のyoutube動画はとても助かります。

いつもお世話になっておりますー
モンテカルロ法による導出
モンテカルロ法は、乱数を利用する計算方法です。
国家試験である「ITパスポート」や「基本情報技術者試験」にも出題されます。
素粒子の運動をシミュレーションするために開発された手法で、ウラムって人が考案したとのことです。

むずかしそーって思うけど
実は簡単にできちゃうー
ジョン・フォン・ノイマンさん
モンテカルロ法って名前を付けたのは、ジョン・フォン・ノイマンさんです。
モンテカルロさんじゃないんですねw
さて、ジョン・フォン・ノイマンさんを聞いたことがあるならOKです。
20世紀科学史における最重要人物で、いろんな分野で超活躍された方です。
現在のコンピュータも「ノイマン型コンピュータ」と云いますからね。

ノイマンさんは知っておこー
pythonで作ってみましょう
円周率を求めますが、面積を使う手法で行きます。
そして面積を「縦×横」みたいな数値計算ではなく、点の数で表します。
点を打つ場所をランダムにします。そこで乱数を使うわけです。
では、pythonで以下を打ち込んで実行してください。円周率でますよ!
import random
cntmax=1000000
cnt2 =0
for i in range(1,cntmax+1):
x=random.uniform(0,1)
y=random.uniform(0,1)
if x**2+y**2 <= 1:
cnt2=cnt2+1
print(4*cnt2/cntmax)
コピペでおっけー
一応説明
えー、どうせ学生は眠くなるので、カットしてもらってOKですw
ほんとに短く説明できるならすれば良いですが、
「プログラムで円周率計算できた。よくわからんけど」って体験だけで充分だと思います。
別のサイト様に丁寧な説明がありますので、ここでは投げやりでw
一度説明したんですけど、寝るんすよ。「メンドイ」とか言われました(キレ気味
- 平面の座標(x,y)にランダムに点を落とします。
- x=0~1、y=0~1とします。
- その点の総数は、一辺が1の正方形の面積に相当します。ここではcntmaxが総数です。
- 落とした点の座標(x,y)がx**2+y**2<=1を満たす場合は、半径1の1/4円の面積に相当します。ここではcnt2で数えています。
- cnt2/cntmax=1/4*πとなります。
- よって4*cnt2/cntmax=πとして円周率を求めています。

めんどくせーって言われてから
二度と教えてないですねー
まとめ | 円周率の歴史
ここまで読んで頂きありがとうございます!

ありがとー
円周率を導出した歴史です。
現在は企業のスーパーコンピュータで計算してるでしょうが、
昔は一個人が世界記録を持っていたんですね。
プログラムをかじると、整数型だの単精度実数だの倍精度実数だのでてきますが、
どうやって桁を管理してるんでしょうね。と、考えは絶えません。

じゃ またー


