三重ループを使って、「フェルマーの最終定理」をしてみましょう。
フェルマーの最終定理は、330年も証明ができなかった数学問題です。
ループ文だけの簡単なpythonプログラムで迫ります。
プログラムの便利さと数学の面白さを少しでも体験できればと思います。
以下の動画を、6:40ぐらいまで見ると良いです。
youtubeには、数学・物理・歴史・環境などなどを解説してくれる動画があって面白いですね。

ヨビノリさんの
魔法陣もお薦めー
▼事前に読んで欲しい記事▼
フェルマーの最終定理とは
下記の式を満たす、自然数x,y,zの組み合わせは、nが3以上のとき、全然ない。
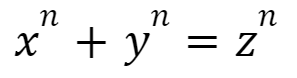
自然数ってのは、1,2,3・・・って「正の整数」です。
この証明するということは、
「nが3以上の全ての自然数、x,y,zの全ての自然数について、成り立つかどうかを証明する」
ということです。
あらゆる数を計算しないで証明をする数学、すごいですね。
1995年に証明されました。
照明されたのは、フェルマーさんが亡くなってから330年とのことです。
n=2の式
フェルマーの最終定理によると、n=2の時は満たすx,y,zは存在するはずです。
ってことで、手計算でも良いし、プログラムでも良いので計算してもらいましょう。
「2乗の式で成立したら、x,y,zの数を表示してね」
表示されるべき答えをいくつか教えて、確認するってのでも良いかもしれません。
pythonコード
for x in range(1,100):
for y in range(1,100):
for z in range(1,100):
if x**2 + y**2 == z**2:
print(f"{x} {y} {z}") 下記のようにずらーーーーーーーと、結果がでるはずです。
3 4 5
4 3 5
5 12 13
6 8 10
7 24 25
8 6 10
8 15 17
9 12 15
9 40 41
10 24 26
(省略)
80 18 82
80 39 89
84 13 85
84 35 91
コピペでおっけー
できたー?
n=3の式
三重ループ
ここから、フェルマーの最終定理に迫ります。
定理によると、n=3の時は満たすx,y,zが存在しないはずです。
「プログラムを3乗の式に改造してください。探す範囲は1~99ぐらいでOKです」
これだけで良いです。
for x in range(1,100):
for y in range(1,100):
for z in range(1,100):
if x**3 + y**3 == z**3:
print(f"{x} {y} {z}") 成立するx,y,zはないので、結果は何も表示されませんね。
「1から99の範囲内で存在しないだけ」とも思うので、範囲を広げてみたりしましょう。
どんどん計算にかかる時間が増えますね。

結果出たら大発見だねー
いやバグだよー
プログレスバーでかっこよく!
探索範囲を広げると、計算じかんが増えて、今どこまで計算がすすんでいるかわかりません。
なので、
プログレスバーをつけてみましょう。
tqdmというライブラリを使いますが、
大抵はインストールされていないので、pipコマンドでインストールします。
# Anaconda や Visual Studio Codeなどの環境の場合
pip install tqdm# google colaboratory や Jupyter Notebookなどの環境の場合
!pip install tqdmpythonのソースコードです。
from tqdm import tqdm
for x in tqdm(range(1,100)):
for y in range(1,100):
for z in range(1,100):
if x**3 + y**3 == z**3:
print(f"{x} {y} {z}") プログレスバーがあるとカッコイイですよねw
100%|██████████| 99/99 [00:00<00:00, 111.60it/s]こんな感じで、学生さんに
- 数学の問題をコンピュータで力技で解く手法
- プログラムで数学の問題に挑戦した体験
- このような数学を江戸時代の人達がやってきたこと
そんなことを伝えられたら良いなと思います。

人力で大変だったのを
コンピュータで力業ー
計算範囲が正しいか確認しよう
今までのプログラムには、「探索漏れ」があります。
自分としても難しい話なので飛ばしてもOKです。
さっきのプログラムでは、xを1~99、yを1~99、zを1~99しています。
(ちょっと面倒なので、xを1~100、yを1~100、zを1~100と考えましょう。)
左辺は、1+1=2から、1000000+1000000=2000000まで計算されます。
- 左辺は、1~2000000の範囲になりますが、
- 右辺は、1~1000000までしか計算していません
なので、右辺の探索範囲も、2000000までと広くとるべきです。
126の3乗が2000376なので。
from tqdm import tqdm
for x in tqdm(range(1,100)):
for y in range(1,100):
for z in range(1,126): ##################変更箇所
if x**3 + y**3 == z**3:
print(f"{x} {y} {z}") 
人間が確認しないとねー
計算誤差を考える必要がある
別の計算方法を考え、変数zについてのループをなくして、三重ループから二重ループにしてみましょう。
「左辺を3乗根(1/3乗)して、それが整数になるか確認する」というプログラムにすると、zのループがなくても大丈夫になりそうです。
from tqdm import tqdm
for x in tqdm(range(1,100)):
for y in range(1,100):
# (x**3 + y**3)**(1/3): ##### 左の値が整数であるかを判定するコードにする。
print(f"{x} {y} {z}") 問題は、三乗根した時に、コンピュータの演算誤差がでてこないかが気になるので、その確認もする必要があります。
x=5
x=x**3
x=x**(1/3)
print(x)でもコードを実行してみると、x=5に完全には戻らないです。
4.999999999999999これが、コンピュータの計算誤差です。
したがって、「(x**3 + y**3)**(1/3)が整数であるか」というのは危ないです。
数学には無理数という無限に数が続く数がありますし、コンピュータは2進数でわたしたちは10進数と違う数も使っています。それらがもたらす計算誤差にも気を配ることが大事です。

プログラムが動いた!だけでなく
「正しく」動いているかも見よー
まとめ | プログラムで本質を学ぼう
ここまで読んで頂きありがとうございます!

ありがとー
たがが、三重ループのプログラム色んな苦労もありました。
でも、ちょっと突き詰めるだけで、学べることはたくさんありましたね。
- 数学問題をプログラムで「力技」で解いたみた
- 「プログレスバー」を表示してカッコよくなった
- 「計算が正しい範囲」で行われるか確認する大事さを知った
- コンピュータは「計算誤差」があるので注意が必要だと知った
動画にあった「オイラーの予想」などについては、以下の記事をどーぞ!

じゃ またー



