フェルマーの最終定理に関係して「オイラー予想」をPythonでやってみましょう。
簡単な計算をして、解の探索探索回数を減らす工夫をしてみようと思います。
「オイラーの予想」についてです。15:50~16:48ぐらいをご覧ください。
この記事は、「Pythonでフェルマーの最終定理」の続きです。

よろしくー
▼事前に読んで欲しい記事▼
オイラーの予想
オイラーの予想とは
オイラーさんって1700年代の数学者がいます。
以下のような式を満たす、自然数x,y,z,wの組み合わせはない、って予想をしました。
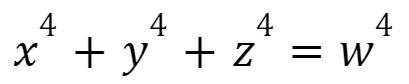
なんですけど、これは予想が外れたようです。
x=2682440 y=15365639 z=18796760 w=20615673
これをpythonで確認してみましょう。
探索だと時間がかかるので、
「左辺と右辺の値をそれぞれ計算して表示してね」
x= 2682440
y=15365639
z=18796760
w=20615673
x = x**4 + y**4 + z**4
w = w**4
print(x)
print(w)
print(x-w)180630077292169281088848499041
180630077292169281088848499041
0ということで、限られた範囲を探索しても、外側に答えがあることもあるんですね。
1986年にコンピュータによる計算で発見されました。
200年も見つからなかった答えがある場合もあるので、
あらゆる数を計算することなく、あらゆる数について証明をする数学をする必要がある。
数学ってすごいですね。
5乗や6乗もあるので探索してみよう
5乗が成立する数は、x=27, y=84, z=110, w=133, v=144です。
150以下の探索で足りるので、やってみましょう。
from tqdm import tqdm
for x in tqdm(range(1,150)):
for y in range(x,150):
for z in range(y,150):
for w in range(z,150):
for v in range(1,150):
if x**5 + y**5 + z**5 + w**5 == v**5:
print(f"{x} {y} {z} {w} {v}") うそです。めちゃ時間かかって途中で止めました。
これからは、計算回数を減らす工夫を考えます。
計算回数を減らす改良をしてみよう
オイラー予想の5乗版は、探索時間がすごくかかります。
計算回数を減らすような改良を考えていきましょう。
重複する探索をしないようにする
フェルマー最終定理でも思ったのですが
出る答えが、x=3, y=4, z=5 とか x=4, y=3, z=5 みたいに入れ替わったのもでてくるので、
無駄な計算をしていますね。
なので、
x≦y≦z≦v≦wの範囲を探すように改良したい
と思いました。
from tqdm import tqdm
for x in tqdm(range(1,150)):
for y in range(x,150):
for z in range(y,150):
for w in range(z,150):
for v in range(w,150):
if x**5 + y**5 + z**5 + w**5 == v**5:
print(f"\n{x} {y} {z} {w} {v}") でもまだすごい時間かかりそうです。
計算回数を減らしてみる
vを振っている時に、x,y,z,wの値は変わりません。
いままでのプログラムだと、vが変わった時にも毎回計算をしています。
左辺が変わらないのにね。
じゃぁ、左辺が変わる、つまり、
wが変わった時にだけ、x,y,z,wの5乗の和を計算するようにしてみましょう。
from tqdm import tqdm
for x in tqdm(range(1,150)):
for y in range(x,150):
for z in range(y,150):
for w in range(z,150):
v1 = x**5 + y**5 + z**5 + w**5 # wが変わった時に左辺を計算する。
for v in range(w,150):
if v1 == v**5:
print(f"\n{x} {y} {z} {w} {v}") 少し速くなりました。
探索範囲を限定する
右辺はw=1~150を毎回5乗しています。
右辺の計算回数を減らしてみたいです。
左辺の5乗和がでたら、その値になりそうなwだけ計算ことを考えます。
左辺の5乗和を計算して、とりあえず変数v1に格納します。
このv1の1/5乗が自然数になっていれば良いんですよね。
しかし、変数v1を1/5乗すると計算誤差が発生する場合があります。
下のコードの計算結果は、ぴったり5にはなりません。コンピュータの計算には誤差があります。
# 計算誤差
x=5
x=x**5
x=x**(1/5)
print(x)5.000000000000001よって、
その値の周辺を探索することにします。
5.000000000000001の場合は、4~6を探索します。
4.999999999999999の場合は、3~5を探索します。
これでvの探索は3回だけになりました。
from tqdm import tqdm
for x in tqdm(range(27,29)):
for y in range(84,87):
for z in range(110,112):
for w in range(133,135):
v1 = x**5 + y**5 + z**5 + w**5
st = v1**(1/5)
st = int(st)
for v in range(st-1,st+2):
if v1==v**5:
print(f"\n{x} {y} {z} {w} {v} {v1} {v**5}") 実行すると、まぁ待てるかなぁと。
必要な時だけ計算する
計算誤差は小さいのと、探したい値は自然数(小数点以下が0)なのを考えて、
整数からのずれが小さいときだけ、「解なんじゃね?」ってことで計算することにします。
つまり、左辺の1/5乗が5.5や5.7の時に、右辺が5や6とかの整数になるわけはないので無視します。
左辺の1/5乗が5.000000000000001とか4.999999999999999だったら、w=4~6を探そうかなってしたい。
from tqdm import tqdm
for x in tqdm(range(1,150)):
for y in range(x,150):
for z in range(y,150):
for w in range(z,150):
v1 = x**5 + y**5 + z**5 + w**5
st = v1**(1/5)
if st-int(st)<0.00001: #計算誤差が小さい時だけ探索する。
st = int(st)
for v in range(st-1,st+2): #計算誤差があるから、周囲を探してみる。
if v1==v**5:
print(f"\n{x} {y} {z} {w} {v} {v1} {v**5}") 必要な計算だけをする
5.000000000000001の時も4.999999999999999の時も、5だけを候補として計算すれば良いですよね。
今までは、vの探索回数は3回(v=4, 5, 6)でしたが、1回(v=5)計算するだけにします。
from tqdm import tqdm
for x in tqdm(range(1,150)):
for y in range(x,150):
for z in range(y,150):
for w in range(z,150):
v1 = x**5 + y**5 + z**5 + w**5
st = v1**(1/5)
if st-int(st)<0.00001:
v = round(st,0) # 四捨五入
if v1==v**5:
print(f"\n{x} {y} {z} {w} {v} {v1} {v**5}") round()について
実は、round()は完全な四捨五入ではないです。
でもこの計算には影響ないです。
2.5や3.5のような「5」が絡むときに偶数丸めをするようです。
2.5は2に、3.5は4になります。
これは、5を必ず切り上げると、1~4の4個が切り捨て、5~9の5個が切り上げになって不平等になるからって統計的な理由です。
ですが、今回の計算では関係ありません。
for x in [0.5, 1.5, 2.5, 3.5, 4.5, 5.5]:
print(f"{x} ->{round(x)}")

