数学問題をPythonプログラミングで解きましょう。
今回は連立方程式です。ループ文の基本として良い課題ですよ。
xなりyなりの係数を合わせて足し算引き算して、xかyだけの式にして片方ずつ決める解法ですね。
係数が複雑だと手計算では工夫が必要になったり、xとyに加えてzも加わると大変です。
今回は連立方程式を満たす数を探すってプログラミングをしてみます。
※厳密には連立方程式ではないものもあります。
▼事前に読んで欲しい記事▼
二元一次方程式
問1:今回使うプログラムのひな型
以下の2式を成立させるxとyの値を求めます。
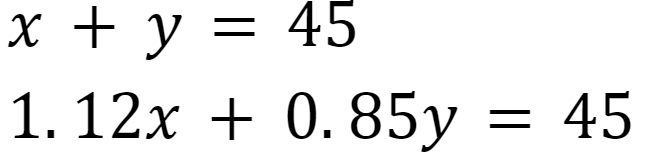
少数の掛け算かぁと嫌になる問題ですね。
手計算で工夫する場合は下記の記事を参考に。
Pythonでどう解くかというと力業ですw
xとyのあらゆる数で、2式が成立するxとyを探します。
最初の課題なので、プログラムソースを学生にも模写してもらうが良いと思います。
- x=1, y=1で左辺を計算する
- 左辺と右辺が等しいか判定する。
- 以上を2つの式について行う。
- 以上を2つの式で左辺=右辺が成り立たなかったら、次の数を試す。
- x=1, y=2をやって、x=1, y=3をやって、x=1, y=4をやって・・・yを探しきったら、
- x=2, y=1をやって、x=2, y=2をやって、x=2, y=3をやって・・・yを探しきったら、
- x=3, y=1をやって・・・・
- yを探しきって、xも探しきったら終わり。
- xとyは1~50の範囲を探すこととします。
さて、答えです。今回はこの形をちょろっと改造するだけなので簡単な課題です。
# https://www.soranokillingtime.com/study/simultaneous-equations/
for x in range(1,50):
for y in range(1,50):
if x+y==45 and x*1.12+y*(1-0.15)==45:
print(f"x={x} y={y}")x=25 y=20さて、この数式を立てた問題文は下記です。
去年の男子と女子の人数は合計で45人でした。
今年は男子の人数は去年から12%増え女子は15%減り、その合計は45人のままでした。
ここで問題です。
今年の男子と女子の人数は何人でしょうか?
そらの暇つぶしch
式のxとyは「去年の」男子と女子の人数になっていますので、xとyから「今年の」人数にする必要があります。
print(f"x={x*1.12} y={y*(1-0.15)}")計算誤差が入ってしまいますが、まぁ良いでしょう。
x=28.000000000000004 y=17.0この記事をとおして、下記の教育的高価を行っていきます。
- 問題文を読んで連立方程式を立てる能力
- 「プログラムのひな型」を改良する能力
競技プログラミングでも必要となってきます。
問2:今回の探索プログラムの弱点
以下の2式を成立させるxとyの値を求めます。
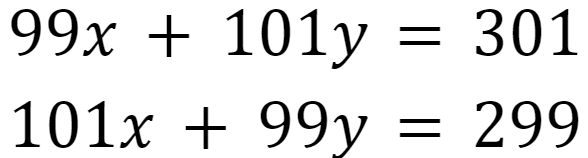
これも、二桁や三桁の掛け算かぁとげっそりするところです。
手計算による工夫は下記の記事です。
学生には、下記のアナウンスでOKです。
- 「問1のプログラム」を改良してxとyを求めてください。
- 探す範囲はxもyも1~10で大丈夫です。(これは言わなくてもまぁOKです)
方程式を見てif文の条件を変更するだけです。
余裕があれば、探索範囲を1~50だったのを1~10に変えれば良いです。
# https://www.soranokillingtime.com/study/simultaneous-equations-2/
for x in range(1,10):
for y in range(1,10):
if 99*x+101*y==301 and 101*x+99*y==299:
print(f"{x} {y}")
- rangeで探す範囲の外に答えがあったら見つからない。
- 答えが整数以外(少数がある)だったら見つからない。
今回はしませんが、本来は行列及び行列式を使った「クラメルの公式」などを使うのが通常です。
三元一次方程式
二元一次方程式でプログラムで満たす数を探すプログラムは分かったので、
三元一次方程式をしてみましょう。変数がxとyに、さらにzが加わります。
問題文を読んで、立式をする能力を育成しましょう。
問3:三重ループが組めるか
三種類のビンの重さをそれぞれ求める問題です。
下記の記事の図を見てください。
プログラムを作る上での、学生へアナウンスは下記です。
変数を統一しましょう。
- 小瓶の個数をa、中瓶の個数をb、大瓶の個数をcとおきます。
- 探索範囲は1~10で大丈夫です。
最初の問題なので、連立方程式を見せるのはOKです。
学生が三重ループとif文の条件追加ができるように挑戦をサポートしましょう。
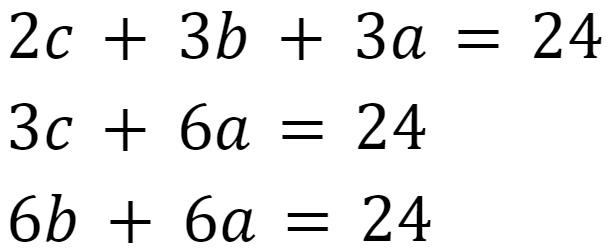
# https://www.soranokillingtime.com/analytical-puzzle/large-medium-small-bottles/
for a in range(1,10):
for b in range(a+1,10):
for c in range(b+1,10):
if c*2+b*3+a*3==24 and c*3+a*6==24 and b*6+a*6==24:
print(f"小={a/10} 中={b/10} 大={c/10}")小=0.1 中=0.3 大=0.6問4:立式できるか
下記の記事の問題「絵」を読んで取り組みます。
課題は下記です。
- 変数について統一します。
- みかんは「o(オー)」、リンゴは「a」、サクランボは「c」です。
- まず連立方程式を立ててください。
- プログラムで満たす、o,a,cを探索してください。
- 範囲は1~30で大丈夫です(伏せてもOKです)。
- o, a, cが探索できたら問題の式を計算してください。
もしつまるようでしたら、「サクランボを1個ではなく1粒で数えるように」とヒントを出しもOKです。
個人的なお願いがあります。
私は、プログラムの変数にローマ字を使うことに反対です。
今回の変数を、mikan, ringo, sakuranboとしないで欲しいです。
英語に慣れさせてください。日本では中学・高校と英語がカリキュラムに導入されています。最近は小学校もですよね。いつまでも「英語が苦手で」と言わせないでください。英語が苦手だろうが、長年習ってきたわけです。使う機会を与えて練習するのが教育です。
苦手ではなく、慣れるんです。慣れるためには触れるんです。その触れる機会を奪う教育には、個人的で恐縮ですが強く反対します。
今後、学生たちは社会人になり、プログラムや情報収集でも、英語のマニュアルやニュースを見ることになります。プログラムの関数、OSのコマンドも英語です。
今回はorange, apple, cherryにすると綴り間違いなどが起こりそうなのと、if文の条件が見にくくなるため、頭文字だけにしました。
成り立たせたい3式は下記です。
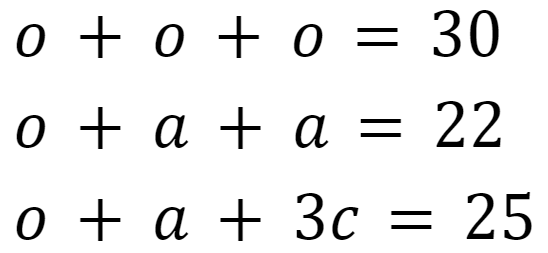
算出したい数式は下記です。
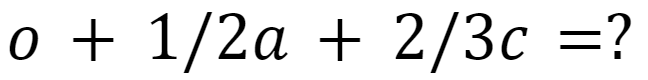
# https://www.soranokillingtime.com/interesting_math_problems/calculated-with-fruits/
for o in range(1,30):
for a in range(1,30):
for c in range(1,30):
if o+o+o == 30 and o+a+a==22 and o+a+c==25:
print(f"orange={o} apple={a} cherry={c}")
print(o+1/2*a+2/3*c)orange=10 apple=6 cherry=9
19.0問5:自分でif文を追加できるか
(実は、連立方程式ではないですが、見逃してくださいね。)
手計算での解法は下記です。
課題は下記です。
- 問題文を読んでプログラムを完成させてください。
- 方程式を満たす変数(a,b,c)が見つかったら、どれが一番重いのかを判定して、結果を表示させてください。
- 探索範囲は自由にして大丈夫です。
方程式が成立する数を見つけたら、更に条件文で一番重いものを判定するプログラムを追加できるかですね。
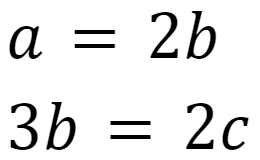
# https://www.soranokillingtime.com/analytical-puzzle/which-is-the-heaviest/
for a in range(1,10):
for b in range(1,10):
for c in range(1,10):
if a == b+b and b+b+b == c+c:
print(f"{a} {b} {c}")
if a > b and a > c:
print("一番重いのは、a")
elif b > c and b > a:
print("一番重いのは、b")
elif c > a and c > b:
print("一番重いのは、c")実は今回は、「連立方程式とは言い難い」式で、解が無数にあります。
4 2 3
一番重いのは、a
8 4 6
一番重いのは、aでもa,b,cの相互関係は変わらないので、常にaが一番重い組み合わせが解となります。
四元一次方程式
最後に変数を四つにしてみましょう。
もう手計算はしたくないですね。
問6:探索範囲を考えてみる
もう問題文を見て立式、プログラミングはできそうですね。
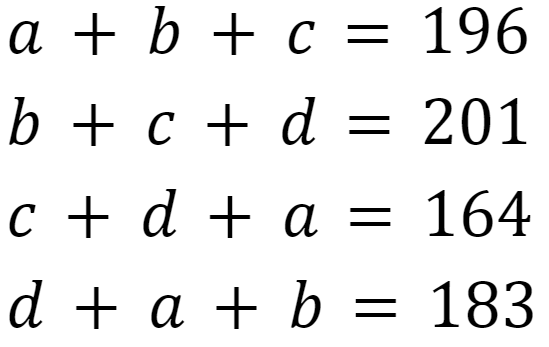
探索範囲については下記を伝えてみましょう。
- A,B,C,Dが取り得る最大値を考えて、探索範囲を設定してみてください。
探索範囲については、いろんな考え方があると思います。
- 人間の体重のギネス記録は500だから、1~500にする。
- お相撲さんの平均体重が157ぐらいなので、1~160ぐらいにしてみる。
- b,c,dの合計が201だから、1~200にしてみる。数学的ですね。
# https://www.soranokillingtime.com/interesting_math_problems/body-weight/
for a in range(1,200):
for b in range(1,200):
for c in range(1,200):
for d in range(1,200):
if a+b+c==196 and b+c+d==201 and c+d+a==164 and d+a+b==183:
print(f" {a} {b} {c} {d}")答えは2分ぐらいで見つかりますが、プログラムが終わるまでは3分ぐらいかかります。
47 84 65 52まとめ
今回は、連立方程式を題材に、for文の力業で数学問題を解いてみました。
こんな力業がコンピュータのすごいところだと思います。
また、手計算とプログラムでの解き方の違いだったり、今回のプログラムは整数しか探していないという弱点も分かったかもしれません。
現実問題を題材として、数式を立式し、プログラムで解く一連の手順ができたと思います。
値の探索範囲についても言及しまし、探索に時間がかかることも体験しました。


